Pitagoras (
gr. Πυθαγόρας,
Pythagoras) (ur. ok.
572 p.n.e. na
Samos lub w
Sydonie[1], zm. ok.
497 p.n.e. w
Metaponcie) –
grecki matematyk,
filozof,
mistyk
kojarzony ze słynnym twierdzeniem matematycznym nazwanym jego imieniem.
Z relacji anonimowego autora wiadomo, że Pitagoras żył 104 lata
[2], ale większość opisów wzmiankuje jedynie około 80 lat. Według jednej z wersji zmarł w Metaponcie w domu zapaśnika
Milona, ocalony z pogromu Krotony, zaś innej - rewolty tej nie przeżył. Według wielu źródeł jego żoną była
Teano, z którą miał dwóch synów: Telangesa i Menezarcha
[3].
[4][5][6]
Podróże
Jamblich opisał jego podróż do
Egiptu i uprowadzenie do
Babilonii, gdzie miał zapoznać się z tamtejszą matematyką, jednak powoływanie się na wiedzę
Egiptu i
Babilonii było w starożytności częstym zabiegiem mającym zwiększyć wiarygodność danego mistrza. Do Egiptu udał się za namową
Talesa, którego był uczniem
[7]. Sam Pitagoras podobno mówił, że w Egipcie żyją mędrcy, a on jest tylko filozofem (czyli
miłośnikiem mądrości). W ten sposób Pitagoras wprowadził określenie
filozof.
Jamblich opisał to tak: "W czasach zaś, w których żył Pitagoras, On
jeden w umiłowaniu mądrości przewyższył wszystkich innych. Dlatego
nazywano Go mianem filozofa, zamiast mędrca"
[8]. Z kolei
Bruno Kiciński
twierdzi, iż "Pierwszy Pitagores nazwał się filozofem, to jest
miłośnikiem mądrości mówiąc że nazwisko Sophos czyli mędrca, Bogu tylko
przystoi"
[3]
W późniejszym czasie, "Gdy [Pitagoras] osiągnął czterdziesty rok życia i gdy spostrzegł, iż rośnie tyrania
Polikratesa, uznawszy, że nie godzi się mężowi wolnemu znosić despotyzmu i ograniczeń, udał się do Italii"
[9].
Nie zgadza się to jednak z wersją Jamblicha, według której w Egipcie
spędził 22 lata, a potem 12 lat w Babilonii, skąd powrócił na Samos w
wieku lat 56
[10].
Szkoła Pitagorasa
Szkoła
Założył w
Krotonie szkołę
pitagorejczyków w roku
529 p.n.e., będąc m.in. spadkobiercą idei
Ferekydesa z Syros i
Hermodamasa z Samos
[11]. Od ok.
509 p.n.e.
przebywał w Metaponcie, choć według niektórych tylko 40 dni. Wykłady
odbywały się w jego domu, a na swoich uczniów wybierał osoby zdolne do
milczenia, które byłyby w stanie zachowywać w tajemnicy jego nauki. Za
nieprzyzwoite uważał "uliczne filozofowanie", co mogło się jednak
sprowadzać do plotek na temat wychowania lub zwykłej niedyskrecji
[12]. Nauczał ukryty przed słuchaczami, dla których miało być to jedynie formą próby
[13], stosując przekaz przy pomocy symboli, tak jak czynili to Egipcjanie
[14].
We wspólnotach pitagorejczyków, w czasie pięcioletniej nauki, adept nie posiadał żadnej własności prywatnej.
"Tę więc zasadę [Pitagoras] najlepiej ze wszystkich ludzi
urzeczywistnił, eliminując ze sposobu życia to co prywatne, powiększając
natomiast [zakres] wspólnoty, [ogarniając nią] rzeczy najdrobniejsze
będące przyczynami zamętu i niepokoju. Wszystko bowiem było wspólne dla
wszystkich i nikt nie miał niczego własnego"
[15].
Potwierdza to także inny fragment dzieła tego samego autora. "Nakazał
więc, by dobra pitagorejczyków były wspólne i by pędzili wspólny żywot
przez całe życie; natomiast pozostałym polecił, by każdy miał swój
majątek, lecz by schodzili się razem dla wspólnych nauk"
[16].
Jamblich zaś opisał to nieco inaczej. Przez pięcioletni okres, gdy
adept był poddawany próbie milczenia, jego majątek był użytkowany
wspólnie przez polityków, zarządców i prawodawców wspólnoty
[17].
Wcześniej, po bezpośrednim wyborze kandydata przez Pitagorasa, nowo
przyjęty był w ramach próby przez trzy lata dla odmiany lekceważony
[18], choć tego etapu Diogenes nie wzmiankuje.
Pitagoras był wyznawcą
orfizmu,
który praktykowano we wszystkich greckich koloniach: "Mówi się zaś na
ogół, iż Pitagoras był naśladowcą Orfeusza, jeśli chodzi o sposób
mówienia i myślenia"
[19]. Członkowie wspólnoty w podobny sposób oddawali cześć boską Pitagorasowi, czcząc go np. jako
Apollina Pytyjskiego
[20].
Najbardziej pewnym źródłem informacji o moralności Pitagorasa mogłyby być "
Złote wiersze",
których jest co najmniej przypuszczalnym autorem, choć nie wiadomo jak
wiele z tej treści pozostało takie, jak w wersji oryginalnej. Trudno
odróżnić poglądy Pitagorasa od przemyśleń następców ze
szkoły pitagorejskiej
często przypisywanych przez nich mistrzowi. Pitagoras cenił bardzo
przyjaźń i mimo, że Diogenes przypisał sentencję zupełnie innym
filozofom greckim, podobno "On to pierwszy powiedział, że przyjaciele
powinni mieć wszystko wspólne i że przyjaciel jest [dla człowieka]
drugim ja"
[21].
Pitagoras sformułował także „
twierdzenie Pitagorasa”,
ale ewentualny dowód musiał być oparty na pomiarze, a nie rachunku
algebraicznym, którego wówczas jeszcze nie znano, zresztą twierdzenie to
w oryginalnej wersji żadnych kwadratów nie wzmiankuje: "złożył w
ofierze wołu z ciasta pszennego, kiedy to odkrył, że przeciwprostokątna
trójkąta prostokątnego równa jest przyprostokątnym"
[22]. Jest również wynalazcą
skali muzycznej.
Pitagorejczycy głosili idee
nieśmiertelności oraz
wędrówki dusz,
zaś drugi pogląd zanikł wśród bardziej współczesnych "wyznawców" i
pochodził raczej od orfików. Sam Pitagoras wymieniał kilka postaci
historycznych, z którymi identyfikował się korzystając z wyznawanej
idei.
Pitagorejczycy potrafili czytać i pisać, prowadzili notatki, jak
również stosowali formę częstego rachunku sumienia (znanego przecież
nawet Egipcjanom). Według "Złotych wierszy" Pitagoras doradzał dobre
wychowanie i opiekę nad rodzicami i bliskimi oraz modlitwę.
Żywoty Pitagorasa
podają szereg przykładów, z których wynika, że pitagorejczycy byli
ludźmi dbającymi o równowagę ducha, nie nawykłymi do kłamstwa i
kradzieży, słownymi, niosącymi ofiarnie pomoc innym pitagorejczykom.
Jako jeńcy byli czasem wypuszczani, gdyż zgodnie z daną obietnicą
wracali:
"Dionysios zaś, gdy niektórzy powiadali, że [pitagorejczycy] w niebezpieczeństwie bynajmniej nie dochowują sobie wierności, chcąc ich poddać próbie, tak uczynił: pochwyconego Fintiasa przyprowadzono przed oblicze tyrana. Dionysios zaś oskarżył go oto, że uknuł przeciwko niemu spisek; dowiedziono mu tego i skazano na śmierć. [Fintias] zaś prosił Dionysiosa, by - skoro tak ma być - dał mu resztę dnia na uporządkowanie spraw majątkowych, jego i Damona, który był mu przyjacielem
i wspólnikiem. [Fintias] bowiem, jako starszy, wziął na siebie wiele spraw związanych z majątkiem. Prosił zatem by wolno mu było odejść, dając Damona jako zakładnika. Gdy Dionysios na to przyzwolił, przywołany Damon usłyszawszy co zaszło, stawił się jako zakładnik, by pozostać, dopóki Fintias nie wróci. Dionysios był wstrząśnięty tym, co zaszło. Ci zaś, którzy doprowadzili do owej próby, szydzili z Damona jako pozostawionego na pastwę losu. Lecz gdy słońce chyliło się ku zachodowi, przybył Fintias, by ponieść śmierć [co widząc] wszyscy osłupieli. Dionysios zaś, obejmując i całując [obu] mężów, prosił, by przyjęli go jako trzeciego do ich przyjacielskiego związku. Oni jednak, jakkolwiek [Dionysios] usilnie o to błagał, w żaden sposób nie chcieli się na to zgodzić"[23].
Siłę odzyskiwali grając, głównie na cytrze, i śpiewając; "Uważał, że
także muzyka przynosi wielkie korzyści zdrowiu, jeśli ktoś uprawia ją we
właściwy i przystojny sposób....Dla poprawienia stanu duszy posługiwali
się też wybranymi wierszami
Homera i
Hezjoda"
[24].
Muzyką starali się także opanowywać emocje innych, ale przede wszystkim
"Jeśli przeto któregoś z nich ogarnął gniew, czy smutek, czy inne tego
rodzaju uczucie, usuwali się na bok i każdy sam starał się po męsku
opanować i uśmierzyć ów efekt."
[25].
Pitagoras zalecał dbałość o równowagę ducha i jak wynika z relacji
Porfiriusza "nikt Go nigdy nie widział śmiejącego się ani płaczącego"
[26], a według Jamblicha cechował go "spokój pogodny i nieporównywalny z niczyim"
[27].
Skutkiem symbolicznego nauczania, zasad i trwania tajemnicy język
pitagorejczyków mógł być nieco niezrozumiały dla osób postronnych: "A
jeśli się zdarzyło, że znalazł się [w tym gronie] ktoś z ludzi obcych,
rzec by można profanów, wówczas mówili zagadkami i symbolami, których
przykładem są znane [sentencje], jak na przykład "nie gaś ognia
mieczem", i inne tego rodzaju symbole, które same przez się wydają się
być starczym marudzeniem."
[28].
Sam Pitagoras miał być podobno widywany w wielu miejscach
równocześnie i choć opisy takie znane są z czasów współczesnych, nie
wiadomo czy przyczyna miałaby być podobna, czy jest to jedynie
przesłanka za życzeniowością lub niedosłownością relacji Porfiriusza i
Jamblicha, które nie mogły chyba dotyczyć powszechności jakiegoś
wizerunku lub nawet jedynie pisma; "A i to, że tego samego dnia
przebywał wspólnie i rozmawiał z przyjaciółmi w Metaponcie w Italii i w
Tauromenion na Sycylii, co poświadczali wszyscy zgodnie, [a miejsca te]
dzieli wiele stadiów drogi lądem i morzem nie do przebycia w ciągu wieli
dni"
[29].
Źródła nie wzmiankują by Pitagoras potrafił podglądać lub kontaktować
się z innymi na odległość, choć podobno był przewidujący, zatem
prezentowany opis dotyczy pewnie różnych, być może nawet podobnych,
osób, tym bardziej, że uczeń jego, któremu płacił za to, że ten pobierał
od niego naukę, nazywał się tak samo.
Dalekowzroczność Pitagorasa umożliwiała mu przepowiadanie trzęsień
ziemi, a przypisywano mu także "szybkie oddalanie epidemii, umiejętność
natychmiastowego uśmierzania gwałtownych wiatrów i burz, jak też
uspokajania wzburzonych fal morskich i rzecznych, by jego przyjaciele
mogli łatwo je przekraczać.
Empedokles z Akragantu i
Epimenides z Krety, jak też Abarys Hiperborejczyk nauczywszy się tego, często i w wielu miejscach czynili podobnie."
[30].
Pitagoras miał być rzekomo w posiadaniu
złotej strzały Abarisa, na której miał podróżować po świecie. Strzałę tę podarował Pitagorasowi
Abaris
w zamian za naukę; "niektórzy sądzili, że również Pitagoras korzystał z
tej umiejętności, kiedy obcował z przyjaciółmi tego samego dnia w
Metaponcie i w Tauromenion"
[31]. Wersję taką potwierdza także Porfiriusz
[32].
W domu Pitagorasa najwyraźniej znajdowała się też złota rzeźba, którą
pewnie po podboju Kortony zakopano w piwnicy, a której części są
wzmiankowane w opracowaniach ("złote biodro" i "złota broda"). Sam
kruszec nie miał podobno dla Pitagorasa bardzo dużej wartości.
Porfiriusz i Jamblich będący neoplatończykami mogli także, raczej
nieświadomie, cytować opisy cyniczne (gdyż posługiwali się jedynie
materiałami źródłowymi) jak np. przykład osoby czyniącej nazwę
przedmiotu z wyniku pomiaru jego powierzchni, być może jedynie po to by
ośmieszyć lub utrudnić ewentualne naśladownictwo innej niż platońskiej
filozofii (litery alfabetu były w owym czasie używane również jako cyfry
i liczby i łatwo było wprowadzić taką dwuznaczność), wychwalając
również np. wspominaną już słowność i grzeczność jeńców. Podobnie
zresztą było z rzekomą niespożywalnością bobu, którą obydwaj autorzy
gloryfikują podając argumenty mistyczne, natomiast wiadomo, że był
treścią posiłków, choć spożywany w krajach śródziemnomorskich bez
gotowania może powodować
fawizm[33].
Pitagoras unikał gotowanych pokarmów, zatem być może również bobu;
"odznaczał się taką czystością obyczajów i niechęcią do zabijania i
zabijających, iż nie tylko powstrzymywał się od [spożywania] istot
żywych", lecz, co brzmi trochę zabawnie a nawet mało wiarygodnie, "nie
zbliżał się w ogóle do kucharzy i myśliwych"
[34].
Niektóre z cyfr (1,2,3) miały znaczenie symboliczne, zaś podobne znaczenie siódemce przypisał raczej
Klemens Aleksandryjski[35].
Z lektury Porfiriusza, Jamblicha i Diogenesa nie wynika by liczb tych
było aż tak dużo, jak życzyliby sobie tego autorzy niektórych z
współczesnych opracowań. Pogląd o tym, że Pitagoras jako pierwszy
nadawał liczbom znaczenie symboliczne wydaje się być natomiast
powszechny. Liczby służyły Pitagorasowi także do wróżbiarstwa.
Innym przykładem takich dwuznaczności są rozmowy Pitagorasa ze
strumieniem, którego odpowiedzi słyszeli podobno wszyscy ze wspólnoty;
"Dalej, i to przekraczając kiedyś z towarzyszami rzekę Nessos, przemówił
do niej, a rzeka wyraźnie i jasno odpowiedziała: "Bądź pozdrowiony,
Pitagorasie", co wszyscy słyszeli"
[36],
choć Porfiriusz opisał to nieco inaczej: "Opowiadano również, że
odezwał się kiedyś do rzeki Kaukasos przeprawiając się przez nią wraz z
wieloma przyjaciółmi; a rzeka głosem jasnym i dźwięcznym przemówiła doń:
"Bądź pozdrowiony, Pitagorasie", co wszyscy słyszeli"
[37].
Od Diogenesa Laertiosa wiadomo także, że Pitagoras, który jak wynika z
innych opisów naśladował Orfeusza, nabrał podobno jakieś osoby
przebywając kilka dni pod ziemią, a następnie chwalił się znajomością
wszystkich istotnych wydarzeń, których w tym czasie nie mógł być
świadkiem, zaś szczegółów dowiedział się z pamiętnika poproszonej o
sporządzenie takich zapisków osoby
[38].
Nie jest zatem pewnym, czy Porfiriusz i Jamblich zacytowali opisy
jakiejś formy iluzji, czy miałaby to być pułapka mająca zachęcić do
sprawdzenia lub dorównania takim "umiejętnościom", głos ukrytej osoby
odpowiadającej na pozdrowienie, czy kłamstwo. Postrzeganie takie może
kojarzyć się z udręczoną świadomością niewolników, którzy nie odważyliby
się być może zrozumieć tego co usłyszeli, choć we wspólnocie Pitagorasa
efekt taki możliwy był do uzyskania raczej poprzez wspólne i
jednoczesne ćwiczenia wyobraźni, znoszące prywatność w sferze duchowej.
Los części grup niewolników w starożytnej Grecji był nieco lżejszy
niż w innych krajach i lepszy niż proponował zabraniający im śmiechu i
radości Platon w swoim
Państwie – mogli być traktowani jak
rodzina, zaś niewolnicy państwowi zawierać małżeństwa; przyjęcie nowo
nabytego niewolnika domowego do rodziny odbywało się przez obrzucanie go
ciastem, co było formą zabawy, ale gdzie indziej takie zwyczaje nie
były praktykowane
[39]. Od
Diogenesa Laertiosa
wiadomo, że niektórzy, jak Arystoteles, byli za ich los, a także za
wykształcenie odpowiedzialni, i wyzwalali. Podobnie Pitagoras odesłał do
kraju swego pochodzenia wolnego
Zamolksisa, z którym się przyjaźnił, a którego dostał w prezencie. Mimo sympatii Pitagorasa do osób różnych stanów, zasady
Złotych wierszy doradzają jednak by na przyjaciół wybierać sobie tych "którzy w cnocie są najdoskonalsi".
Pitagoras miał mieć także wpływ na zachowanie zwierząt: "Złapawszy
bowiem, jak opowiadają, niedźwiedzicę daunijską, która wyrządzała wiele
szkód mieszkańcom [okolicy], przetrzymał ją przez jakiś czas, a
następnie nakarmiwszy plackiem i orzechami wypuścił, by nie tykała
więcej żadnej istoty żywej. Ta zaś poszła prostą drogą w góry i lasy i
nie widziano nigdy, by zbliżyła się nawet do zwierzęcia. Zobaczywszy zaś
w Tarencie byka jedzącego bób na mieszanym pastwisku, podszedł do
pasterza i poradził mu, by powiedział zwierzęciu, aby powstrzymało się
od bobu; a gdy pasterz zadrwił z Niego mówiąc, że nie umie mówić byczym
językiem, sam zbliżył się do zwierzęcia i naszeptał mu do ucha; [byk]
nie tylko natychmiast zostawił bób, lecz również w przyszłości nigdy
bobu nie tykał"
[40].
Pitagorejczycy zakładali istnienie
harmonii sfer, znając być
może okresy obiegu planet wokół Słońca, których ruchowi nie towarzyszą z
wiadomych współczesnym fizykom względów żadne dźwięki. Natomiast
właśnie Porfiriusz przypisał boskości Pitagorasa ich słyszenie, choć
pewnie byłby to jednak problem dla tłumacza, podobnie jak zamienne
stosowanie w potocznym języku polskim słów "widzieć" i "rozumieć": "sam
zaś rozumiał harmonię wszechświata, mogąc słyszeć ogólną harmonię sfer i
gwiazd poruszających się w ich kręgach; my nie słyszymy tej harmonii ze
względu na słabość naszej natury....Stwierdzał, że dźwięki, jakie
wydaje siedem gwiazd stałych i ta z planet, którą z racji położenia
wobec nas nazywają
Przeciwziemią (
Antichthon), to dziewięć Muz"
[41]
Z poglądami Pitagorasa zwykło się łączyć wczesny model Wszechświata przypisywany przez Arystotelesa
Filolaosowi[42],
według którego Ziemia, wszystkie widoczne planety, ale także Słońce i
wzmiankowana w opisie Porfiriusza Przeciwziemia miały obiegać tzw.
ogień centralny. System ten, mimo że wywarł wpływ na tok badań Kopernika, o czym astronom wspomniał w
De Revolutionibus, nie był w rzeczywistości heliocentryczny. Słońce poruszało się po orbicie kołowej, podobnie jak planety
[43]. Z opisu Arystotelesa wynika także, że
Antychton
został wprowadzony celowo by zwiększyć liczbę planet do dziesięciu,
ponieważ dziesiątka była uważana przez pitagorejczyków za doskonałą.
Część interpretatorów skłania się jednak do przeciwnego poglądu,
twierdząc, że ogień centralny byłby w układzie planetarnym jedenastym, a
zatem nadmiarowym, obiektem.
Według Janiny Gajdy Krynickiej
[44] szkoła Pitagorasa przetrwała do III w. p.n.e.. Późniejsze wspólnoty, np.
Archytasa, skłaniały się ku
ascezie i medycynie, bardzo różniąc się od siebie w różnych koloniach greckich.
Na początku I tysiąclecia (być może nawet w pierwszym wieku n.e.)
upowszechniła się bardziej współczesna wersja światopoglądu
pitagorejskiego, tzw.
neopitagoreizm.
Pogrom Krotony
Hermetyczność bractwa pitagorejskiego spowodowała olbrzymią zawiść
niedopuszczonych przez Pitagorasa do jego wtajemniczeń i wspólnoty. Ta
właśnie część ludności Krotony wystąpiła przeciw Pitagorejczykom w dniu
święta Muz, podburzona również brakiem korzyści z wojny, którą prowadził
lud Krotony z Sybaris i oskarżeniami Pitagorasa o dążenie do
jedynowładztwa.
"Gdy zgodnie ze zwyczajem siedział na zebraniu w domu Milona, ktoś,
kogo nie uznano godnym zaproszenia, z zemsty dom podpalił. Niektórzy
jednak twierdzą, że zrobili to sami mieszkańcy Krotony, lękając się, że
Pitagoras zamierza objąć rządy tyrańskie"
[45]
W czasie buntu spalono 35 członków wspólnoty
[46],
zaś miasta (regionu) nie wymierzyły buntownikom żadnej kary. Bezkarność
ta nie pojawia się natomiast w relacji Jamblicha: "Pitagoras udał się
do Delos do Ferekydesa Syryjczyka, swego nauczyciela, by - złożonego
chorobą ... pielęgnować i [po śmierci] pochować. Wtedy to ci, których
pitagorejczycy wykluczyli ze swego grona... napadli na nich i wszystkich
spalili; sami zaś zostali przez Italczyków ukamienowani i porzuceni bez
pogrzebu."
[47].
Dopiero po śmierci przywódcy buntu pozwolono ocalonym powrócić do miasta
[48].
Diogenes podaje jednak, iż rewolta odbyła się w czasie wojny
prowadzonej wówczas z zupełnie innym miastem południowej Italii -
Akragas na Sycylii
[49].
Diogenes wzmiankuje także, że Pitagorasów było naprawdę czterech, choć
filozof i oskarżony o dążenie do samowładztwa miały by być zupełnie
innymi osobami. Domniemane miejsce pochówku Pitagorasa nie jest znane, a
żaden ze wzmiankowanych tekstów nie określa tego w żaden sposób.
Jamblich podkreśla, że
Pitagoras już od dzieciństwa ściągał na siebie ludzką zawiść. Jak długo rozmawiał i obcował z każdym, kto do Niego przyszedł, spotykał się z ogólną życzliwością; kiedy jednak zaczął rozmawiać tylko ze swoimi uczniami, ustała powszechna dlań życzliwość. [Niektórzy] zgodnie uważali, że jako obcy przybysz jest kimś gorszym; inni nienawidzili go za to, że ich rodacy cenią go bardziej od innych i sądzili, że szkoła [pitagorejska] knuje przeciwko nim zdradę."[50]. Przed wzbudzaniem zazdrości przestrzegają także "Złote wiersze".
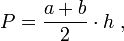
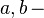długości podstaw;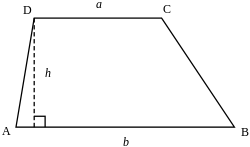
wysokość, czyli odległość między podstawami
matematyk, urodzony i zmarły w Syrakuzach; wykształcenie zdobył w Aleksandrii. Był synem astronoma Fidiasza i
prawdopodobnie krewnym lub powinowatym władcy Syrakuz Hierona II.
Życiorys 
Leonhard Euler (ur. 15 kwietnia 1707 w Bazylei, zm. 18 września 1783 w Petersburgu) - szwajcarski matematyk i fizyk;
był pionierem w wielu obszarach obu tych nauk. Większą część życia spędził w Rosji i Prusach. Jest uważany za jednego
z najbardziej produktywnych matematyków w historii.
Dokonał licznych odkryć w tak różnych gałęziach matematyki jak rachunek różniczkowy i całkowy oraz teoria grafów.
Wniósł duży wkład w rozwój terminologii i notacji matematycznej, szczególnie trwały w dziedzinie analizy matematycznej.
Jako pierwszy w historii użył na przykład pojęcia i oznaczenia funkcji. Opublikował wiele ważnych prac z zakresu
mechaniki, optyki i astronomii. 
