Ciekawostki 2

Duże liczby

Wszyscy dobrze znamy nazwy: dziesięć, sto, tysiąc, milion, miliard, bilion, biliard... a co dalej?  

Poniżej przedstawiam system nazewnictwa liczb obowiązujący w Polsce i jeszcze w kilku krajach (Wielkiej Brytanii, Niemczech), ale uwaga: w innych, np. we Francji, Hiszpanii, Stanach Zjednoczonych system jest zupełnie inny, co prowadzi czasem do nieporozumień...

• milion         10⁶    1 000 000
• miliard        10⁹    1 000 000 000
• bilion          10¹²   1 000 000 000 000
• biliard         10¹⁵   1 000 000 000 000 000
• trylion         10¹⁸   1 000 000 000 000 000 000
• tryliard        10²¹   1 000 000 000 000 000 000 000
• kwadrylion  10²⁴   1 000 000 000 000 000 000 000 000                                                        
• kwadryliard 10²⁷                                                                                                               
• kwintylion    10³⁰                                                                                                                          
• kwintyliard   10³³ 
• sekstylion     10³⁶ 
• sekstyliard   10³⁹ 
• septylion      10⁴² 
• septyliard     10⁴⁵ 
• oktylion        10⁴⁸ 
• oktyliard       10⁵¹ 
• nonylion        10⁵⁴ 
• nonyliard      10⁵⁷ 
• decylion        10⁶⁰ 
• wicylion        10¹²⁰ 
• trycylion       10¹⁸⁰ 
• kwadragilion   10²⁴⁰ 
• kwinkwagilion   10³⁰⁰ 
• sekswilion    10³⁶⁰ 
• septagilion    10⁴²⁰ 
• oktogilion     10⁴⁸⁰ 
• nonagilion    10⁵⁴⁰ 

Autor: Sylwia Pawlas o 15:12

Ciekawostki 1

Magiczne kwadraty to liczby tak ułożone, że suma każdej kolumny, rzędu oraz na przekątnej jest równa tej samej liczbie.

Najmniejszy kwadrat magiczny (3 x 3) to:

Każdy wiersz, każda przekątna i każda kolumna po zsumowaniu daje tu liczbę 15. Taką liczbę matematycy nazywają „stałą magiczną”.

Kwadraty magiczne mogą być różnej wielkości na przykład 4 x 4,        5 x 5, 6 x 6 itd.

Kwadraty magiczne znali już przed paru tysiącami lat Chińczycy i Hindusi. Jak głosi chińska legenda najprostszy kwadrat magiczny objawiony został cesarzowi Yü na grzbiecie żółwia w XXIII wieku p.n.e.

W Europie kwadraty magiczne upowszechnił w początkach XV wieku Grek Moscopulos.

Graniastosłup

Graniastosłup – wielościan, którego wszystkie wierzchołki są położone na dwóch równoległych płaszczyznach, zwanych podstawami graniastosłupa i którego wszystkie krawędzie leżące poza tymi podstawami są do siebie równoległe.Wysokość graniastosłupa to odległość między jego podstawami.
Graniastosłup prosty to graniastosłup o prostokątnych ścianach bocznych – ściany boczne są wówczas prostopadłe do podstawy. W przeciwnym wypadku jest to tzw. graniastosłup pochyły.
Graniastosłup prawidłowy to graniastosłup prosty o podstawach będących wielokątami foremnymi.
Graniastosłup archimedesowy (czasem nazywany pryzmą) to graniastosłup o krawędzi podstawy tej samej długości co wysokość. Graniastosłupy archimedesowe tworzą obok antygraniastosłupów jedną z dwóch nieskończonych serii wielościanów półforemnych.

Trapez

Trapez – czworokąt mający przynajmniej jedną parę równoległych boków nazywanych podstawami, pozostałe noszą nazwę ramion; odległość między podstawami to wysokość. Niektórzy autorzy^[1][2][3] definiują trapez jako czworokąt posiadający tylko jedną parę boków równoległych, tzn. uważają, że równoległobok nie jest trapezem.
Suma miar kątów leżących przy tym samym ramieniu dowolnego trapezu jest równa 180°.
gdzie:

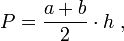
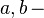• długości podstaw;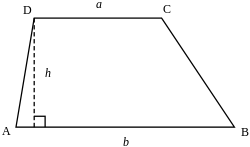
• wysokość, czyli odległość między podstawami

Gauss

Życiorys
Carl Friedrich Gauß (Gauss) (ur. 30 kwietnia 1777 w Brunszwiku, zm. 23 lutego 1855 w Getyndze) - niemiecki matematyk, fizyk, astronom i geodeta. Uznawany jest za jednego z twórców geometrii nieeuklidesowej. Uważany jest za jednego z największych matematyków, przez sobie współczesnych określany był mianem księcia matematyków (łac. princeps mathematicorum). Jego podobizna widniała na dziesięciomarkowym banknocie.

Ciekawostki
Gauss jako pierwszy podał algorytm obliczania daty Wielkanocy, która jak wiadomo jest świętem ruchomym i przypada w pierwszą niedzielę po pierwszej pełni księżyca, następującej po równonocy wiosennej. Być może Gauss, młody człowiek o wybitnym, "ścisłym" umyśle, wybrałby inny zawód niż matematyka - posiadał on wybitne uzdolnienia językowe i rozważał dalsze studia języków klasycznych - gdyby nie drobny przypadek. W 1796 udało mu się udowodnić, że jest możliwa konstrukcja foremnego 17-kąta przy użyciu tzw. narzędzi Euklidesa, to znaczy cyrkla i linijki.

Geniusz matematyczny Carla dał o sobie znać bardzo wcześnie. Jako malec sam nauczył się czytać, wypytując starszych o wymowę liter alfabetu, a także opanował samodzielnie proste rachunki. Często później wspominał, ze nauczył się rachować, zanim jeszcze zaczął mówić. Nauczyciel matematyki w szkole, do której poszedł Gauss. Lubił mięć sporo spokoju na lekcjach, toteż dawał dzieciom do wykonania mozolne rachunki. Kiedy Gauss znalazł się w klasie arytmetyki, na jednej z pierwszych lekcji nauczyciel polecił dzieciom zsumować wszystkie liczby od 1 do 40. Ledwie skończył dyktować zadanie, mały Gauss położył na katedrze swoja tabliczkę z rozwiązaniem. Inne dzieci męczyły się bardzo długo i wszystkie pomyliły się w rachunkach. Tymczasem młody Carl spostrzegł od razu, ze w tym szeregu liczb suma liczb pierwszej i ostatniej, drugiej i przedostatniej itd. wynosi zawsze 41, toteż mnożąc 41 przez liczbę par, 20, otrzymał prawidłowy wynik 820.

Banach

   
Życiorys
Stefan Banach (ur. 30 marca 1892 w Krakowie, zm. 31 sierpnia 1945 we Lwowie) - polski matematyk, jeden z przedstawicieli lwowskiej szkoły matematycznej. Stefan Banach urodził się 20 marca 1892 roku w Krakowie. Banach to nazwisko matki Katarzyny. Jego ojcem był urzędnik krakowskiej dyrekcji kolejowej, Greczek. Wychowywał się w domu właścicielki pralni, gdzie został oddany zaraz po urodzeniu. Jego rodzice nie interesowali się nim. Zapoczątkował współczesną analizę funkcjonalną, wniósł istotny wkład w rozwój teorii topologicznych przestrzeni wektorowych, zajmował się ponadto teorią liczb rzeczywistych i szeregów ortogonalnych. W czasie okupacji niemieckiej był karmicielem wszy w lwowskim Instytucie Badań nad Durem Plamistym R. Weigla. Zmarł przed repatriacją. Za najważniejszą pracę Banacha uważa się Thorie des oprations linaires (Teoria operacji liniowych, 1932). Był jednym z inicjatorów wydawnictw Studia Mathematica i Monografie Matematyczne.

Ciekawostki
Andrzej Turowicz, benedyktyn i jednocześnie profesor matematyki, absolwent Uniwersytetu Jagiellońskiego, wykładający na Politechnice Lwowskiej, opowiadał, że Banach mimo, że nie skończył studiów wyższych, to uzyskał tytuł doktora, i to w sposób dość niezwykły. Banach, gdy rozpoczął pracę we Lwowie, był już autorem wielu doniosłych rezultatów. Jednak na uwagi, że powinien wkrótce przedstawić pracę doktorską, odpowiadał, że ma jeszcze czas. Może uda mu się wymyślić coś lepszego, niż to co osiągnął do tej pory. W końcu zwierzchnicy Banacha się zniecierpliwili - ktoś spisał jego najnowsze rezultaty, co zostało uznane za znakomitą pracę doktorską. Przepisy wymagały również egzaminu. Pewnego dnia zaczepiono Banacha na korytarzu Uniwersytetu Jana Kazimierza: "Czy mógłby pan wpaść do dziekanatu, są tam jacyś ludzie, którzy mają pewne problemy matematyczne, a pan na pewno potrafi im wszystko wyjaśnić". Banach udał się zatem do wskazanego pokoju i chętnie odpowiedział na wszystkie pytania, nieświadom tego, że właśnie zdaje egzamin doktorski przed komisją specjalnie w tym celu przybyłą z Warszawy.

Descartes

Życiorys
Kartezjusz (fr. René Descartes, łac. Renatus Cartesius, ur. 31 marca 1596 w La Haye-en-Touraine w Turenii, zm. 11 lutego 1650 w Sztokholmie) francuski filozof, matematyk i fizyk, jeden z najwybitniejszych uczonych XVII wieku, uważany za prekursora nowożytnej kultury umysłowej.

Ciekawostki
Legenda głosi, że Kartezjusz wpadł na pomysł wprowadzenia współrzędnych do geometrii, leżąc w łóżku i obserwując muchę pełzająca po suficie blisko narożnika. W pewnym momencie "olśniło go", że droga muchy po suficie mogłaby zostać opisana, gdyby znany był związek między odległościami muchy od dwu sąsiednich ścian.